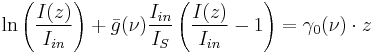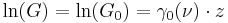Stimulated emission
In optics, stimulated emission is the process by which an electron, perturbed by a photon having the correct energy, may drop to a lower energy level resulting in the creation of another photon. The perturbing photon is seemingly unchanged in the process (cf. absorption), and the second photon is created with the same phase, frequency, polarization, and direction of travel as the original. If the resultant photons are reflected so that they traverse the same atoms or gain medium repeatedly, a cascade effect is produced. Stimulated emission is really a quantum mechanical phenomenon, but it can be understood in terms of a "classical" field and a quantum mechanical atom. The process can be thought of as "optical amplification". It is upon this principle that both lasers and masers function.
Contents |
Overview
Electrons and how they interact with each other and electromagnetic fields form the basis for most of our understanding of chemistry and physics. Electrons have energy in proportion to how far they are on average from the nucleus of an atom. However, quantum mechanical effects force electrons to take on quantized positions in orbitals. Thus, electrons are found in specific energy levels of an atom, as shown below:

When electrons absorb energy either from light (photons) or from heat, they move farther away from the atomic nuclei, but they are only allowed to absorb energy that will land them into specific energy levels. This leads to emission lines and absorption lines.
When an electron is excited, it will not stay that way forever. On average there is a half-life for any particular energy level after which half of the electrons initially in that state will have decayed into a lower state. When such a decay occurs, the energy difference between the level the electron was at and the new level must be released either as a photon or a phonon. When an electron decays without external influence, it is said to be due to "spontaneous emission". The phase associated with the photon that is emitted is random. If a number of electrons were put into an excited state somehow and then left to relax, the resulting radiation would be very spectrally limited (only one wavelength of light would be present), but the individual photons would not be in phase with one another. This is also called fluorescence.
An external electromagnetic field will affect an atom's state - changing the quantum mechanical variables mentioned above. Specifically, the atom will act like a small electric dipole which will oscillate with the external field. One of the consequences of this oscillation is that it encourages electrons to decay to the lowest energy state. When this happens due to the presence of the electromagnetic field from a photon, a photon is released in the same phase and direction as the "stimulating" photon, and is called stimulated emission.
Mathematical Model
Stimulated emission can be modelled mathematically by considering an atom that may be in one of two electronic energy states, the ground state (1) and the excited state (2), with energies E1 and E2 respectively.
If the atom is in the excited state, it may decay into the ground state by the process of spontaneous emission, releasing the difference in energies between the two states as a photon. The photon will have frequency ν and energy hν, given by:
 ,
,
where h is Planck's constant.
Alternatively, if the excited-state atom is perturbed by the electric field of a photon with frequency ν, it may release a second photon of the same frequency, in phase with the first photon. The atom will again decay into the ground state. This process is known as stimulated emission.
In a group of such atoms, if the density of atoms (Number of atoms/m3) in the excited state is given by N, the rate at which stimulated emission occurs is given by:
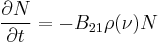 ,
,
where B21 is a proportionality constant for this particular transition in this particular atom (referred to as an Einstein B coefficient), and ρ(ν) is the radiation density of photons of frequency ν. The rate of emission is thus proportional to the number of atoms in the excited state, N, and the density of the perturbing photons.
The critical detail of stimulated emission is that the emitted photon is identical to the stimulating photon in that it has the same frequency, phase, polarization, and direction of propagation. The two photons, as a result, are totally coherent. It is this property that allows optical amplification to take place.
Although most directly related to the discussion of how lasers work, stimulated emission touches on some of the most basic concepts in physics and the interaction of light and matter. It is a very important topic, and key to the understanding of optics specifically and physics in general.
For various reasons, the frequencies of the various photons emitted will not be exactly the same. For example, since the individual atoms in a laser medium are typically at some finite temperature, the Doppler effect will cause the photon wavelengths to vary from atom to atom (although the actual mechanism involved is more complex because of the more complex relationship between relative wavelength of stimulating photon and emitted photon). The spectrum of the photons, then, will not be an infinitesimally thin line, but will be a distribution. This distribution in the spectrum of emitted photons is called "line shape".
Although there are many possible line shapes, it is common to model the spectral line shape function as a Lorentzian distribution:
where
 is the full width at half maximum, or FWHM, in hertz.
is the full width at half maximum, or FWHM, in hertz.
This model is generally valid as long as
and
The line shape function, regardless of the form that it takes, must satisfy the normalization condition of any probability distribution:
which the Lorentzian satisfies.
The peak value of the Lorentzian line shape occurs at the line center:
It is also convenient to define the normalized line shape function:
which is dimensionless, and which has a peak value, also at the line center, of
Stimulated emission cross section
The stimulated emission cross section (in square meters) is
where
- A21 is the Einstein A coefficient (in radians per second),
- λ is the wavelength (in meters),
- n is the refractive index of the medium (dimensionless), and
- g(ν) is the spectral line shape function (in seconds).
Optical amplification
Under certain conditions, stimulated emission can provide a physical mechanism for optical amplification. An external source of energy stimulates atoms in the ground state to transition to the excited state, creating what is called a population inversion. When light of the appropriate frequency passes through the inverted medium, the photons stimulate the excited atoms to emit additional photons of the same frequency, phase, and direction, resulting in an amplification of the input intensity.
The population inversion, in units of atoms per cubic meter, is
where g1 and g2 are the degeneracies of energy levels 1 and 2, respectively.
Small signal gain equation
The intensity (in watts per square meter) of the stimulated emission is governed by the following differential equation:
as long as the intensity I(z) is small enough so that it does not have a significant effect on the magnitude of the population inversion. Grouping the first two factors together, this equation simplifies as
where
is the small-signal gain coefficient (in units of radians per meter). We can solve the differential equation using separation of variables:
Integrating, we find:
or
where
 is the optical intensity of the input signal (in watts per square meter).
is the optical intensity of the input signal (in watts per square meter).
Saturation intensity
The saturation intensity IS is defined as the input intensity at which the gain of the optical amplifier drops to exactly half of the small-signal gain. We can compute the saturation intensity as
where
- h is Planck's constant, and
- τS is the saturation time constant, which depends on the spontaneous emission lifetimes of the various transitions between the energy levels related to the amplification.
 is the frequency in Hz
is the frequency in Hz
General gain equation
The general form of the gain equation, which applies regardless of the input intensity, derives from the general differential equation for the intensity I as a function of position z in the gain medium:
where  is saturation intensity. To solve, we first rearrange the equation in order to separate the variables, intensity I and position z:
is saturation intensity. To solve, we first rearrange the equation in order to separate the variables, intensity I and position z:
Integrating both sides, we obtain
or
The gain G of the amplifier is defined as the optical intensity I at position z divided by the input intensity:
Substituting this definition into the prior equation, we find the general gain equation:
Small signal approximation
In the special case where the input signal is small compared to the saturation intensity, in other words,
then the general gain equation gives the small signal gain as
or
which is identical to the small signal gain equation (see above).
Large signal asymptotic behavior
For large input signals, where
the gain approaches unity
and the general gain equation approaches a linear asymptote:
References
- Saleh, Bahaa E. A. and Teich, Malvin Carl (1991). Fundamentals of Photonics. New York: John Wiley & Sons. ISBN 0-471-83965-5.
See also
- Absorption
- Active laser medium
- Laser (includes a history section)
- Laser science
- Rabi cycle
- Spontaneous emission


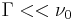












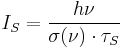
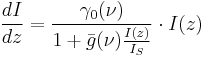
![{ dI \over I(z)} \left[ 1 + \bar{g}(\nu) { I(z) \over I_S } \right] = \gamma_0(\nu)\cdot dz](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/587a942365583aa00db68bb537c8f032.png)